| Table of Contents |
|---|
...
Field | Description | ||||
|---|---|---|---|---|---|
Save as template | Stores all load test input parameters additionally inside an XML template. Later, this template can be used to rerun (repeat) the same load test. | ||||
Execute Test From | selects the Exec Agent or the Exec Agent Cluster from which the load test will be executed. | ||||
Apply Execution Plan | Optionally, an Execution Plan can be used to control the number of users during the load test. The dropdown list shows the Execution Plans' Titles, extracted from all formal valid Execution Plan files (*.exepl files), which are located in the current Project Navigator directory. Note that the titles of invalid Execution Plan files are not shown. If an Execution Plan is selected, then the following input parameters are disabled: Number of Concurrent Users, Load Test Duration, Max. Loops per User, and Startup Delay per User. | ||||
🔴 Number of Concurrent Users | The number of simulated, concurrent users. | ||||
🔴 Load Test Duration | The planned duration of the load test job. If this time has elapsed, all simulated users will complete their current loop (repetition of web surfing session) before the load test ends. Thus the load test often runs a little bit longer than the specified test duration. | ||||
Max. Loops per User | This limits the number of web surfing session repetitions (loops) per simulated user. The load test stops if the limit has been reached for each simulated user.
| ||||
Pacing | Minimum Loop duration per User. Enabling this option sets a minimum time for all in the iteration executed page breaks and URL calls which must be elapsed before the next iteration starts. | ||||
Startup Delay per User | The delay time to start an additional concurrent user (startup ramp of load). Used only at the start of the load test during the creation of all concurrent users. | ||||
Max. Network Bandwidth per User | The network bandwidth limitation per simulated user for the downlink (speed of the network connection from the webserver to the web browser) and the uplink (speed of the network connection from the web browser to the webserver). By choosing a lower value than "unlimited," this option allows simulating web users with a slow network connection. | ||||
Request Timeout per URL | The timeout (in seconds) per single URL call. If this timeout expires, the URL call will be reported as failed (no response from the webserver). Depending on the corresponding URL's configured failure action, the simulated user will continue with the next URL in the same loop, or it will abort the current loop and then continue with the next loop. | ||||
Max. Error-Snapshots | Limits the maximum number of error snapshots taken during load test execution. Either the The maximum memory used to store error snapshots can be configured (recommended - for cluster jobs: value overall cluster members), or the . The maximum number of error snapshots per URL can be configured (not recommended - for cluster jobs: value per Exec Agent). | ||||
Statistic Sampling Interval | statistic sampling interval during the load test in seconds (interval-based sampling). Used for time-based overall diagrams like, for example, the measured network throughput.
| ||||
Additional Sampling Rate per Page Call | Captures the measured response time of a web page when a simulated user calls a web page (event-based sampling). Used to display the response time diagrams in real-time and in the Analyse Load Test Details menu. For endurance tests over several hours, it is strongly recommended that the sampling rate for web pages is set between 1% and 5%. For shorter tests, a 100% sampling rate is recommended.
| ||||
Additional Sampling Rate per URL Call | captures the measured response time of a URL each time when a simulated user calls a URL (event-based sampling). Used to display the response time diagrams in real-time and in the Analyse Load Test Details menu.
| ||||
In addition to capturing the URL calls' response time, further data can be captured by using one of the Add options.
| --- recommended: no additional data are captured
| ||||
Debug Options Choosing any debug option (other than "none") affects that additional information is written to the *.out file of the load test job. The following debug options can be configured: | none - recommended | ||||
Additional Options Several additional options for executing the load test can be combined by adding a blank character between each of the options. The following additional options can be configured. | -multihomed Note 1: It could be needed that TLS SNI (Server Name Indication) must be disabled if a DNS translation table is used. Note 2: The HTTP request header field "Host" is not updated, so it might happen that you could call the Web server with the wrong hostname. -dnssrv <IP-name-server-1>[,<IP-name-server-N>] -dnsperloop | ||||
SSL: specifies which HTTPS/SSL protocol version should be used: | All: Automatic detection of the SSL protocol version. ZebraTester prefers the TLS 1.3 or TLS 1.2 protocol, but if the Web server does not support this, TLS 1.1, TLS 1.0, or SSL v3 is used. This is the normal behavior that is implemented in many Web browser products. v3: Fixes the SSL protocol version to SSL v3. | ||||
Browser Emulation User-Agents and Caching |
| ||||
🔴 Annotation | Enter a short comment about the test run, such as purpose, current web server configuration, and so on. This annotation will be displayed on the result diagrams. |
...
![]() Hint: each Exec Agent always executes load test jobs as separate background processes and is also able to can execute more than one job at the same time. The option Display Real-Time Statistic only means that the GUI opens an additional network connection to the Exec Agent, which reads the real-time data directly from the corresponding executed load test program's memory space.
Hint: each Exec Agent always executes load test jobs as separate background processes and is also able to can execute more than one job at the same time. The option Display Real-Time Statistic only means that the GUI opens an additional network connection to the Exec Agent, which reads the real-time data directly from the corresponding executed load test program's memory space.
...
Alternatively, the load test program can also be scheduled to be executed at a predefined time. However, the corresponding Exec Agent process must be available (running) at the predefined time because the scheduling entry is stored locally inside the Exec Agent jobs working directory, which the Exec Agent itself monitors. Especially if you have started the local Exec Agent implicitly by using the ZebraTester Console - AND if the scheduled job should run on that local Exec Agent, you must keep the ZebraTester Console Window open in order so that the job will be started ¹.
...
Real-time statistics shown in this window are updated every 5 seconds for as long as the load test job is running.
| Note |
|---|
Note:closing this window will not stop the load test job. If you close this window, you can later acquire the load test result or return to this dialogue (if the load test is still running) by clicking on the Jobs icon in the Main Menu or in the Project Navigator window. |
...
Diagram | Description |
|---|---|
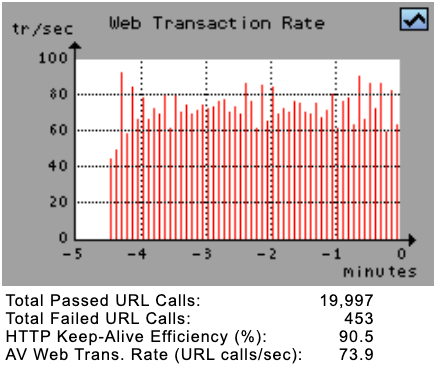
Web Transaction Rate | The Web Transaction Rate Diagram shows the actual number of (successful) completed URL calls per second, counted overall simulated users. By clicking on this diagram, the Response Time Overview Diagrams are shown.
|
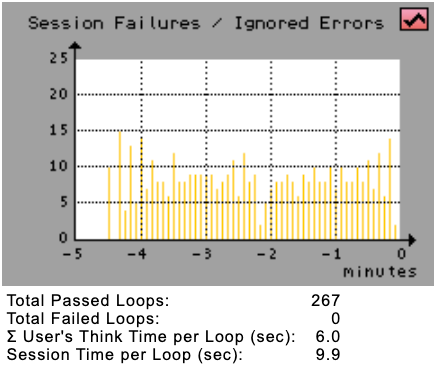
Session Failures / Ignored Errors | The Session Failures / Ignored Errors Diagram shows the actual number of non-fatal errors (yellow bars) and the number of fatal errors (red bars = failed sessions) counted over all simulated users.
|
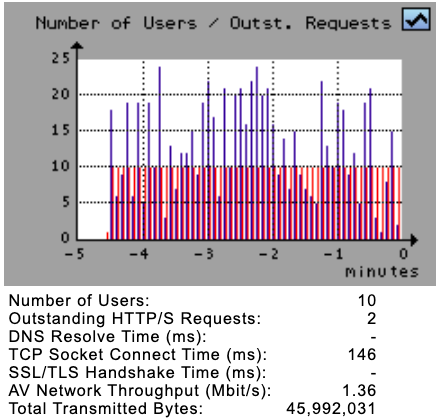
The Number of Users / Waiting Users Diagram shows the total number of currently simulated users (red bars) as well as and the actual number of users who are waiting for a response from the webserver (purple bars). The users waiting for a response is a subset of the currently simulated users. By clicking on this diagram, the Statistical Overview Diagrams are shown.
|
More actual measurement details are available by clicking on the Detailed Statistic button. Especially, an overview of the current execution steps of the simulated users is shown:
...
By clicking on the page's magnifier icon, the The most relevant measured values of the URLs are shown for the selected page by clicking on the page's magnifier icon.
Using this menu, you can also display and analyze error snapshots by clicking on the magnifier icon next to the failure counter. In this way, you can begin analyzing errors immediately as they occur - during the running load test.
By clicking on a URL, the corresponding URL Response Time Diagram is shown.
...
| Allows to select the period, from the current time back to the past, are shown in the diagrams within the response times. |
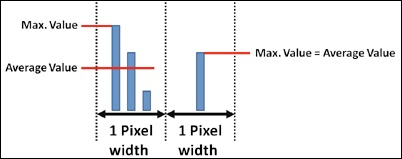
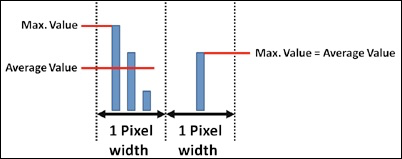
| Allows selecting if the bars inside the diagrams are shown as average values or as max. values. Please note that there is only a difference between the max. values and the average values if multiple measured samples of the response time fall inside the same pixel (inside the same displayed bar):. |
Diagram | Description |
|---|---|
The tables at the right side of the diagrams contain the response times for all URLs of the web page. Also, these response times are either average values or max. values, depending on the selection in the Time Bars drop-down list. However, these values are calculated since the load test was started and always "accurately" measured, which means that they do not depend on the value chosen for the "Additional Sampling Rate per Page Call." | |
You can click on a URL response time to show the corresponding URL Response Time Diagram. | |
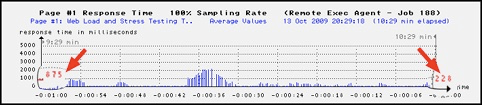
On the left side inside the diagram, the web page's average response time is shown as red-colored text, calculated since the load test was started. But depending on the selected period, this value may not be displayed in every case. On the right side inside the diagram, the last measured value is shown. |
...
All values in this infobox are calculated overall successfully completed calls of the URL, measured since the load test was started. These values are always "accurately" measured, which means that they do not depend on the value chosen for the "Additional Sampling Rate per URL Call."
...
Failure Diagrams: The first diagram shows an overview of what kind of errors did occur at which time, counted overall URLs, and measured since the load test was started. This "basic error information" is always captured in every case, also if no more memory is left to store full error snapshots.
The succeeding diagrams, shown per web page, provide only information at which time errors occurred. The tables on the right side of the diagrams are showing show the number of errors that did occur on the URLs of the web page. You can click on an error counter to show the error detail information (error snapshots) for the corresponding URL. First Error Snapshots: Displays a list of errors that did occur at first (at the start of the load test). By clicking on a magnifier icon, the corresponding error detail information (error snapshot) is shown.
...
After the load test job has been completed, the statistic results file (*.prxres) is stored in the local or remote Exec Agent's job directory. In order to To access this results file, you must transfer it back to the (local) Project Navigator directory from which the load test program was started.
...
If you have specified that an Exec Agent Cluster executes the load test program, the load test program is transmitted to the local cluster job controller, which coordinates coordinating all cluster members (Exec Agents). The cluster job controller creates a cluster job and allocates a cluster job number. The cluster job is now in the state “configured” (ready to run, but not yet started).
...
The number of concurrent users will be automatically distributed across the cluster members, depending on the individual computer systems' capability - called "load factor."
In cases where If the load test program uses Input Files, you are asked for each Input File - if you wish to split the Input File content. This can be useful, for example, if the Input File contains user accounts (usernames/passwords) but the web application does not allow duplicate logins. In this case, each cluster member must use different user accounts. By clicking on the corresponding magnifier icon, you can view how the Input File data would be distributed across the cluster members. If you do not use the split functionality, each cluster member will receive an entire Input File copy.
The distribution of users across the cluster members can also be modified manually; however, this is useful only if a cluster member is currently unavailable (marked with light red background). The cluster job can not be started. In this case, you can assign the unavailable cluster member users to other cluster members and then try to start the cluster job again. This redistribution may take a few seconds to complete.
Alternatively, the load test program can also be scheduled to be executed at a predefined time. However, the local Job Controller process must be available (running) at the predefined time because the scheduling entry for the cluster job is stored inside the Job Controller working directory, which the Job Controller itself monitors. Especially, if If you have started the Job Controller implicitly by using the ZebraTester Console, you must keep the ZebraTester Console Window open in order so that the cluster job will be started ¹. ¹ This restriction can be avoided by installing the local Job Controller as a Windows Service or as a Unix Daemon.
...
The real-time statistics of a cluster job show the most important measured values, similar to the values which are shown in the Real-Time Statistic of Exec Agent Jobs. The cluster job itself contains Exec Agent jobs that the local cluster job controller has created. By clicking on the magnifier icon of a cluster member's magnifier icon, the corresponding Exec Agent job's real-time statistics can be displayed in its own window.
...
By clicking on the magnifier icon, you have can access to the "*.out" and "*.err" files of the corresponding Exec Agent jobs.
...
Usually, you would work inside the Analyze Load Tests menu with the consolidated measurement results only. However, it is also possible to expand the measurement results to access the results of each individual Exec Agent job:
...
This feature can be used to check if all cluster members have measured approximately the same response times; however, variations in a range of ± 20% or more may be normal:
...
Load Test Jobs Menu
...
All load test programs which are started from the Project Navigator are always executed as "batch jobs" by an (external) Exec Agent process or by an Exec Agent Cluster. This means that it is not required to wait for the completion of a load test program on the “Execute Load Test” window: you can close the "Execute Load Test" window at any time, and you can check later the result, or the actual effort, of all load test jobs by using this menu.
If a load test job has been completed, you are disposed to will acquire the corresponding statistic result file (*.prxres). If a load test job is still running, you are disposed to the job's temporary live-statistic window.
...
Item | Description |
|---|---|
Job | Each job has its unique ID, which was automatically assigned when the job was defined. However, the ID is only unique per Exec Agent. Cluster jobs have a known, separate ID (own enumeration counter). |
[Search Icon] | Allows to acquire the statistic result file ( |
[Delete Icon] | Deletes all data (-files) of a completed load test job. Take into consideration Consider that you must first acquire the statistic result file ( |
Date | Displays the date and time when the job has been defined or when the job has been completed, or - for scheduled jobs - the planned point in time when the job will be started. |
State | Displays the current job state: configured (ready to run), scheduled, running, or completed. The state "???" means that the job data are corrupted - you should delete all jobs which have the state "???" because they delay the display of all jobs in this list. |
Load Test Program & Arguments | Displays the name of the load test program and the arguments of the load test program. |
Released from GUI(IP) | Displays the TCP/IP address (remote computer) from which the job has been initiated. |
...
Argument / Parameter | Meaning |
|---|---|
| Number of concurrent users |
| Planned test duration in seconds. 0 = unlimited |
| Request timeout per URL call in seconds |
| Startup delay between creating concurrent users in milliseconds |
| Max. number of loops (repetitions of web surfing session) per user. 0 = unlimited |
| Network bandwidth limitation per concurrent user in kilobits per second for the downlink (web server to web browser) |
| Network bandwidth limitation per concurrent user in kilobits per second for the uplink (web browser to the webserver) |
| Statistical sampling interval in seconds (interval-based sampling). Used for time-based overall diagrams like for example, the measured network throughput |
| Additional sampling rate in percent for response times of web pages (event-based sampling, each time when a web page is called) |
| Additional sampling rate in percent for response times of URL calls (event-based sampling, each time when a URL is called) |
| Max. number of error snapshots per URL (per Exec Agent), 0 = unlimited |
| Max. memory in megabytes which can be used to store error snapshots, -1 = unlimited |
| Replaces the recorded value of the HTTP request header field User-Agent with a new value. The new value is applied for all executed URL calls. |
| Disables writing any date to the |
| Debug failed loops |
| Debug loops |
| Debug headers & loops |
| Debug content & loops |
| Debug cookies & loops |
| Debug keep-alive for re-used network connections & loops |
| Debug information about the SSL protocol and the SSL handshake & loops |
| Forces the Exec Agent(s) to use multiple client IP addresses |
| Using this option in combination combined with the option |
| Use fixed SSL protocol version: |
| The timeout of SSL cache in seconds. 0 = cache disabled |
| Disable support for TLS server name indication (SNI) |
| Effects that the : The load test job uses a known DNS hosts file to resolve hostnames rather than using the underlying operating system's hosts file. Note that you have to ZIP the hosts file together with the load test program's compiled class. To automate the ZIP, it's recommended to declare the hosts file as an external resource (w/o adding it to the CLASSPATH). |
| Effects that the load test job uses specific (own) DNS server(s) to resolve hostnames – rather than using to use the DNS library of the underlying operating system. |
| Enable consideration of DNS TTL by using the received TTL-values from the DNS server(s). This option cannot be used in combination with the option -dnsperloop. |
| Enable DNS TTL by using a fixed TTL-value of seconds for all DNS resolves. This option cannot be used in combination with the option -dnsperloop. |
| Perform new DNS resolves for each executed loop. All resolves are stable within the same loop (no consideration of DNS TTL within a loop). This option cannot be used in combination with the options -dnsenattl or -dnsfixttl. |
| Effects that statistical data about DNS resolutions are measured and displayed in the load test result by using a known DNS stack on the load generators. Note: There is no need to use this option if any other, more specific DNS option is enabled because all (other) DNS options also effect implicitly that statistical data about DNS resolutions are measured. If you use this option without any other DNS option, the (own) DNS stack on the load generators will communicate with the default configured DNS servers of the operating system - but without considering the "hosts" file. |
| Time zone (see Application Reference Manual) |
| Comment about the test-run |
...
To perform these kinds of activities, you must program load test job scripts that are written in the “natural” scripting language of your operating system (Windows: *.bat files, Unix: *.sh, *.ksh, *.csh … files). Inside these scripts, the PrxJob utility is used as the interface to the ZebraTester system. When the Windows version of ZebraTester is installed, the installation kit creates the directory ScriptExamples within the Project Navigator, and this directory contains some example scripts.
...
Rerunning Load Tests Jobs (Job Templates)
Every time when Whenever a load test is started, an additional job definition template file is stored in the actual Project Navigator directory (in XML format). Such a job definition template file contains all configuration data needed to rerun the same load test job again.
...
If you click the corresponding button of a job definition template (XML) file in Project Navigator, the load test job, inclusive of all of its input parameters, is automatically transferred to the Exec Agent or to the Exec Agent Cluster and immediately ready-to-run.
...
Additionally, if you wish to trigger several load test jobs at the same time simultaneously to be ready-to-run (by using only one mouse click), you can zip several templates to one zip archive. After this, click the corresponding button of the zip archive:
...